What Makes a Circle?
An Exercise in the Philosophy of Mathematics
A few years ago in 2017, while on a trip with the rest of my Stake Youth to San Francisco and the surrounding areas, a few buddies and myself were waiting outside the Oakland temple for our bus to arrive to carry us to the next destination. Unknown to us at the time, we would be waiting for about 5 or 6 hours! If I recall correctly, the bus we were supposed to leave on broke down, and a few new ones had to be commissioned in their absence. Naturally, we spent that time as any group of young men would: debating the meaning of "perfection" in the divine nature of God, and whether or not you could construct a "perfect" circle in the real world. Now, we didn't get very far with either topic, but I thought that it was a fun discussion worth remembering.
My friend Quentin posited that it was impossible to create a perfect circle sans a kind of hypothetical mind-world (I forget exactly how he phrased it, but it went something along those lines). I maintained that it was possible, and in fact very easy to do. Being somewhat familiar with mathematical philosophy, I simply said to him that he might be right in the sense that you couldn't, say, construct a perfect circle with any physical material, since you can't arrange an infinite number of atoms in a finite circumference to define a circle as a result of atoms having a size at all. However, because a "perfect" circle has a very straightforward definition, you could use exactly that to construct a "real", "perfect" circle.
To be precise, all there is to a circle is just the collection of every point equidistant (the distance itself being arbitrary) from a central point. So, I posited that you could define a single, infinitesimally small point in physical space*, and then choose an arbitrary distance and define all the points equidistant to that initial point, say a foot. Since it is reasonable to assume that you can have a coordinate system for all of space-time, you could just map your initial point to specific coordinates and also define the points comprising of the circumference by coordinates as well. Here's one simple approach to doing that concretely:
Take any arbitrary point in space using a coordinate system with three dimensions of movement; call it (a, b, c). Now we can use the equation of a sphere:
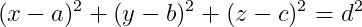
(where d is an arbitrary distance that you can choose) to define a sphere using that point, and then to arrive at a circle simply make a cross section at the desired angle (if orientation matters, that is). So, given a concrete coordinate system in real space, we can construct a real circle. Now, Quentin wasn't having any of this. "Nonsense," he replied. He maintained that any construction that is to be considered "real" must be constructed from some kind of physical material. In this case, since all mathematical objects that exceed zero dimensions require an infinitesimal number of points to be defined, this is simply impossible in the real world. I think we can all agree on that!
*Things like gravity waves may hinder the concept of rigid space-time coordinate systems useless, but that is up for debate.
<< BACK HOME<<